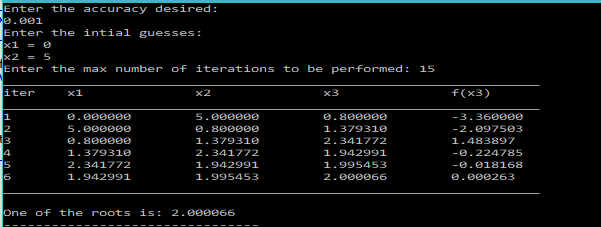
C Program Output: Secant Method. Enter initial guesses: 1 2 Enter tolerable error: 0.00001 Enter maximum iteration: 10 Step x0 x1 x2 f (x2) 1 1.000000 2.000000 2.200000 1.248001 2 2.000000 2.200000 2.088968 -0.062124 3 2.200000 2.088968 2.094233 -0.003554 4 2.088968 2.094233 2.094553 0.000012 5 2.094233 2.094553 2.094552 0.000001 Root is: 2.094552. Working of Muller Method −. Let us assume three distinct initial roots x0, x1 and x2. Now draw a parabola, through the values of function f (x) for the points- x0, x1 and x2. The equation of the parabola, p (x), will be−. P (x )=c+b ( x – x 2)+a ( x – x2)2; where a, b and c are the constants. Now, find the intersection of the parabola.

• C Program For Secant Method With Output Number
• C Program For Secant Method With Output
• C Program For Secant Method With Output Function
• C Program For Secant Method With Output Example
• C Program For Secant Method With Output Data

C program for secant method to find roots of polynomial. Write a program to find the real roots of the following equation using the Secant method: f (x) = 23x^4 -13x^3 + 3x^2 - 5x + 38. Let h = r (i) - r (i-1), where r (i) is the root computed in iteration i of your program. Your program should continue to refine its answer until h. C Program Output: Secant Method. Enter first guess: 0 Enter second guess: 1 Enter tolerable error: 0.000001 Enter maximum iteration: 10. Secant Method. Iteration-1: x2 = -5.000000 and f (x2) = -120.000000 Iteration-2: x2 = 1.315789 and f (x2) = -5.353550 Iteration-3: x2 = 1.610713 and f (x2) = -4.042600 Iteration-4: x2 = 2.520173 and f (x2) = 5.965955 Iteration-5: x2 = 1.978057 and f (x2) = -1.216554 Iteration-6: x2 = 2.069879 and f (x2) = -0.271572 Iteration-7.

Code for SECANT METHOD in C Programming. Program to receive marks in 2 subjects and output whether the student has passed, failed or is allowed to reappear in any.

Controller: CodeCogs

Interface

Secant

doublesecant(	double	(*f)(double)[function pointer]
double	x0 = -1E+7
double	x1 = 1E+7
double	eps = 1E-10
int	maxit = 1000	)

This is a root-finding algorithm which assumes a function to be approximately linear in the region of interest. Eachimprovement is taken as the point where the approximating line crosses the axis. The secant method retains onlythe most recent estimate, so the root does not necessarily remain bracketed.When the algorithm does converge, its order of convergence iswhere C is a constant and is the golden ratio.Let us now derive the actual recurrence relation used with this method.thereforeTo give you a better idea on the way this method works, the following graph shows different iterations in theapproximation process. Here is the associated list of pairs chosen at consecutive stepsThis algorithm finds the roots of the user-defined function f starting with an initial interval [x0, x1] and iteratingthe sequence above until either the accuracy eps is achieved or the maximum number of iterations maxitis exceeded.

References:

• Jean-Pierre Moreau's Home Page, http://perso.wanadoo.fr/jean-pierre.moreau/
• F.R. Ruckdeschel, 'BASIC Scientific Subroutines', Vol. II, BYTE/McGRAWW-HILL, 1981
• MathWorld, http://mathworld.wolfram.com/SecantMethod.html

C Program For Secant Method With Output Number

Example 1

Output:

Parameters

f	the user-defined function
x0	Default value = -1E+7
x1	Default value = 1E+7
eps	Default value = 1E-10
maxit	Default value = 1000

Authors

Lucian Bentea (August 2005)

Source Code

Source code is available when you agree to a GP Licence or buy a Commercial Licence.

Not a member, then Register with CodeCogs. Already a Member, then Login.

C Program For Secant Method With Output

• Trending Categories

C Program For Secant Method With Output Function

• Selected Reading

Secant method is also used to solve non-linear equations. This method is similar to the Newton-Raphson method, but here we do not need to find the differentiation of the function f(x). Only using f(x), we can find f’(x) numerically by using Newton’s Divide difference formula. From the Newton-Raphson formula,

we know that,

Now, using divide difference formula, we get,

By replacing the f’(x) of Newton-Raphson formula by the new f’(x), we can find the secant formula to solve non-linear equations.

Note: For this method, we need any two initial guess to start finding the root of non-linear equations.

Input and Output

Algorithm

Input: Two initial guess for root.

Output: The approximate root of a non-linear equation f(x).

C Program For Secant Method With Output Example

Example

Output

C Program For Secant Method With Output Data

• Related Questions & Answers