C Program Output: Secant Method. Enter initial guesses: 1 2 Enter tolerable error: 0.00001 Enter maximum iteration: 10 Step x0 x1 x2 f (x2) 1 1.000000 2.000000 2.200000 1.248001 2 2.000000 2.200000 2.088968 -0.062124 3 2.200000 2.088968 2.094233 -0.003554 4 2.088968 2.094233 2.094553 0.000012 5 2.094233 2.094553 2.094552 0.000001 Root is: 2.094552. Working of Muller Method −. Let us assume three distinct initial roots x0, x1 and x2. Now draw a parabola, through the values of function f (x) for the points- x0, x1 and x2. The equation of the parabola, p (x), will be−. P (x )=c+b ( x – x 2)+a ( x – x2)2; where a, b and c are the constants. Now, find the intersection of the parabola.
- C Program For Secant Method With Output Number
- C Program For Secant Method With Output
- C Program For Secant Method With Output Function
- C Program For Secant Method With Output Example
- C Program For Secant Method With Output Data
C program for secant method to find roots of polynomial. Write a program to find the real roots of the following equation using the Secant method: f (x) = 23x^4 -13x^3 + 3x^2 - 5x + 38. Let h = r (i) - r (i-1), where r (i) is the root computed in iteration i of your program. Your program should continue to refine its answer until h. C Program Output: Secant Method. Enter first guess: 0 Enter second guess: 1 Enter tolerable error: 0.000001 Enter maximum iteration: 10. Secant Method. Iteration-1: x2 = -5.000000 and f (x2) = -120.000000 Iteration-2: x2 = 1.315789 and f (x2) = -5.353550 Iteration-3: x2 = 1.610713 and f (x2) = -4.042600 Iteration-4: x2 = 2.520173 and f (x2) = 5.965955 Iteration-5: x2 = 1.978057 and f (x2) = -1.216554 Iteration-6: x2 = 2.069879 and f (x2) = -0.271572 Iteration-7.
Code for SECANT METHOD in C Programming. Program to receive marks in 2 subjects and output whether the student has passed, failed or is allowed to reappear in any.
Interface
Secant
| doublesecant( | double | (*f)(double)[function pointer] |
| double | x0 = -1E+7 | |
| double | x1 = 1E+7 | |
| double | eps = 1E-10 | |
| int | maxit = 1000 | ) |
 is a constant and is the golden ratio.Let us now derive the actual recurrence relation used with this method.thereforeTo give you a better idea on the way this method works, the following graph shows different iterations in theapproximation process. Here is the associated list of pairs chosen at consecutive stepsThis algorithm finds the roots of the user-defined function f starting with an initial interval [x0, x1] and iteratingthe sequence above until either the accuracy eps is achieved or the maximum number of iterations maxitis exceeded.
is a constant and is the golden ratio.Let us now derive the actual recurrence relation used with this method.thereforeTo give you a better idea on the way this method works, the following graph shows different iterations in theapproximation process. Here is the associated list of pairs chosen at consecutive stepsThis algorithm finds the roots of the user-defined function f starting with an initial interval [x0, x1] and iteratingthe sequence above until either the accuracy eps is achieved or the maximum number of iterations maxitis exceeded.References:
- Jean-Pierre Moreau's Home Page, http://perso.wanadoo.fr/jean-pierre.moreau/
- F.R. Ruckdeschel, 'BASIC Scientific Subroutines', Vol. II, BYTE/McGRAWW-HILL, 1981
- MathWorld, http://mathworld.wolfram.com/SecantMethod.html
C Program For Secant Method With Output Number

Example 1
- Output:
Parameters
| f | the user-defined function |
| x0 | Default value = -1E+7 |
| x1 | Default value = 1E+7 |
| eps | Default value = 1E-10 |
| maxit | Default value = 1000 |
Authors
- Lucian Bentea (August 2005)
Source Code

Source code is available when you agree to a GP Licence or buy a Commercial Licence.
Not a member, then Register with CodeCogs. Already a Member, then Login.
C Program For Secant Method With Output
- Trending Categories
C Program For Secant Method With Output Function
- Selected Reading
Secant method is also used to solve non-linear equations. This method is similar to the Newton-Raphson method, but here we do not need to find the differentiation of the function f(x). Only using f(x), we can find f’(x) numerically by using Newton’s Divide difference formula. From the Newton-Raphson formula,
we know that,
Now, using divide difference formula, we get,
By replacing the f’(x) of Newton-Raphson formula by the new f’(x), we can find the secant formula to solve non-linear equations.
Note: For this method, we need any two initial guess to start finding the root of non-linear equations.
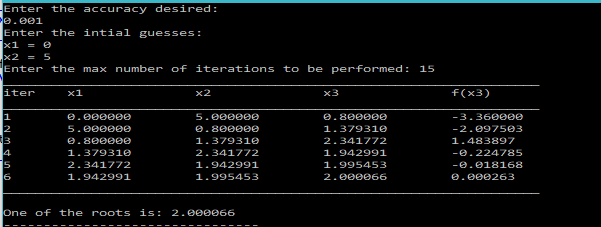
Input and Output
Algorithm
Input: Two initial guess for root.
Output: The approximate root of a non-linear equation f(x).
C Program For Secant Method With Output Example
Example
Output
C Program For Secant Method With Output Data
- Related Questions & Answers